memoization

Complete

lang
/
js

Summary

Basic memory read and write for binary functions

const mem = [];
function read(n, k) {
	return mem[n] === undefined ? undefined : mem[n][k];
}
function write(n, k, value) {
	if (mem[n] === undefined) {
		mem[n] = [];
	}
	mem[n][k] = value;
}

Concept

Trading space for time

avoid doing repeated computation
store results and retrieve it without having to compute it again

Useful in:

fibonacci
n-choose-k

Not useful in:

factorial

Application

n-choose-k

function choose(n, k) {
	return n < k
		   ? 0
		   : k === 0 || k === n 
		   ? 1
		   : choose(n - 1, k) + choose(n - 1, k - 1);
}

oog in time

function mchoose(n, k) {
	if (read(n, k) !== undefined) {
		return read(n, k);
	} else {
		const result = k > n 
					   ? 0 
					   : k === 0 || k === n 
					   ? 1 
					   : mchoose(n - 1, k) +  mchoose(n - 1, k - 1);
		write(n, k, result);
		return result;
	}
}

oog in time and space

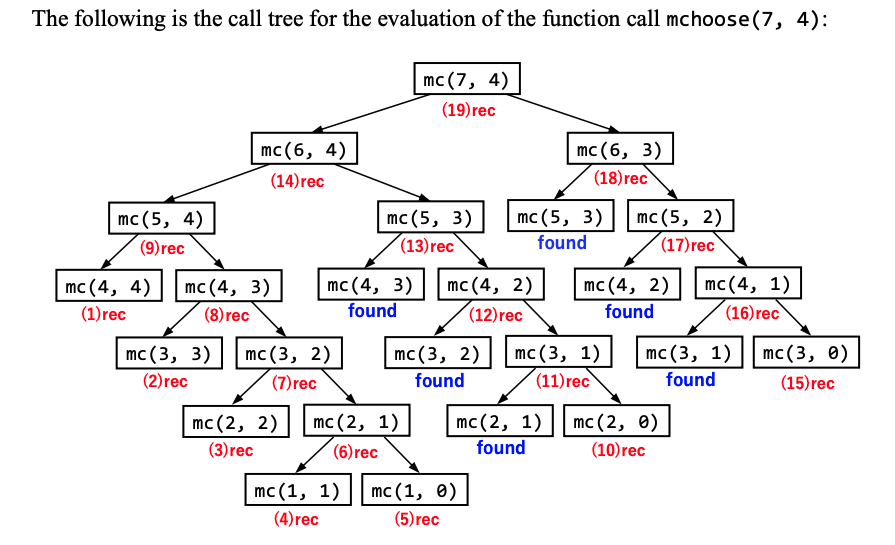
Unary function memoizer and tribonacci series

function memoize(f) {
	const mem = [];
	function mf(x) {
		if (mem[x] !== undefined) { // check if value already exists in memory
			return mem[x];
		} else {
			const result = f(x); // call the function
			mem[x] = result;     // store the result to memory and return
			return result;
		}
	}
	return mf;
}

// trib => 0, 1, 1, 2, 4, 7, ...
const trib = n => n === 0 
				  ? 0
				  : n === 1
				  ? 1
				  : n === 2
				  ? 1
				  : trib(n-1) + trib(n-2) + trib(n-3);
memoize(trib)(5); // -> 7 : but trib is actually not memoized, it makes calls to the un memoized trib()

const mtrib = memoize(n => n === 0 
				           ? 0
						   : n === 1
						   ? 1
						   : n === 2
						   ? 1
						   : mtrib(n-1) + mtrib(n-2) + mtrib(n-3))
mtrib(5); // -> 7 : but acutally memoized this time