sorting II

Work in Progress

Succeeds: sorting

Summary

Comparison based

- bubble sort
- selection sort
- insertion sort
- merge sort
- quick sort

Non-comparison based

- counting sort
- radix sort

Concept

In-place sorting

only require space
exclusively using swap

Stable sorting

relative order of elements with the same value is preserved
using < instead of <= when determining when a swap should occur

Performance

to sort in non-decreasing(ascending but allowing for duplicates) order

	Random	Sorted Non-decreasing	Sorted Non-increasing	Almost Sorted Non-decreasing	Almost Sorted Non-increasing	Many Duplicates
Optimized Bubble Sort
Selection Sort
Insertion Sort
Merge Sort
Quick Sort
Randomized Quick Sort
Counting Sort

bubble and insertion sort are not entirely useless; if we know that the array will already be mostly sorted, they may be faster then merge/quick sort

Unsorted vs Sorted arrays

sorting makes the array easier to work with

Application	Unsorted	Sorted
search	linear search,	binary search,
min/max	linear search,	first and last index,
kth smallest/largest	linear search, quickselect,	k and (last - k) index,
duplicates	nested loops,	duplicates are adjacent,
counting repititons	hash table	duplicates are adjacent,
set intersection/union (without repitition)	nested linear search,	nested binary search, merge from merge sort,
two sum	nested loops,	two pointer approach,
count within range	hash table	two pointer approach,

Application

Swap

java

private static void swap(int a[], int i, int j) { // swap array elements i and j
	int temp = a[i]; // O(1) space
	a[i] = a[j];
	a[j] = temp;
}

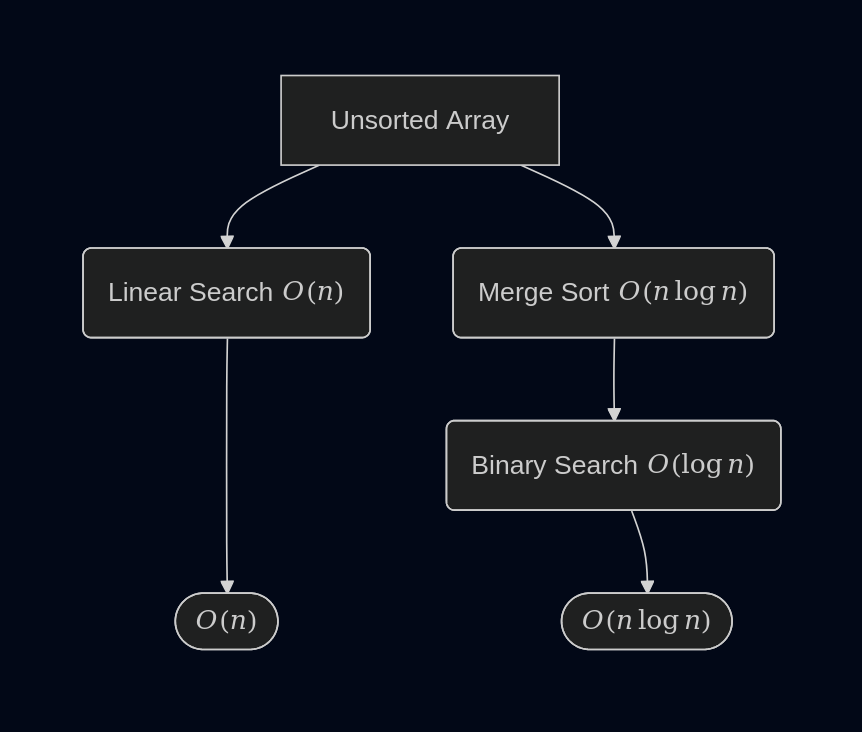
sorting is not necessarily the best solution in all cases

Leetcode: Shortest Unsorted Continuous Subarray

naive sort then check

java

int len = nums.length;
int[] sorted = Arrays.copyOf(nums, len);

Arrays.sort(sorted); // O(n log n)

int l = len, r = 0;

for (int i = 0; i < len; i++) { // O(n)
	if (nums[i] != sorted[i]) {
		l = Math.min(l, i);
		r = Math.max(r, i);
	}
}

return r - l >= 0 ? r - l + 1 : 0;

Minimum swaps to sort an array

each cycle of n elements takes n - 1 swaps