recursion

Complete

Summary

Recursive

js
function factorial(n) {
	return n === 1
	? 1 // Base case
	: n         * factorial(n - 1);
	// Bridge   // Wish
}

creates deferred operations, ie. performs an operation on its recursive function call
delayed statements build up due to the substitution model

js
factorial(4)
4 * factorial(3)
4 * (3 * factorial(2))
4 * (3 * (2 * factorial(1))) // longest chain of deferred opeations, 3
4 * (3 * (2 * 1))
4 * (3 * 2)
4 * 6
24

time and space
num of steps and max num of deferred operations grow linearly with n

Accumulation of defered operations that grows proportionately to the size of the input

Iterative Processes

js
function factorial(n) {
	return iter(1, 1, n);
}
function iter(product, counter, n) {
	return counter > n
	? product
	: iter(counter * product,
		   counter + 1,
		   n);
}

no operations performed on its own function call

js
factorial(4)
iter(1, 1, 4) // no deferred operations are created
iter(1, 2, 4)
iter(2, 3, 4)
iter(6, 4, 4)
iter(24, 5, 4)
24

time but /constant space,
since there are no/constant(ie. happen every recurrence) deferred operations

Concept

Functions that calls itself

  • Base case
  • Wish
  • Bridge
    Gives rise to iterative and recursive processes

Application

Fibonacci series(iterative > recursive solution)

  1. Recursive solution
js
function fib(n) {
	return n <= 1
	? n
	: fib(n - 1) + fib(n - 2); // sum of previous 2 values
}

time grows exponentially, proportionately with the size of the tree

Tree for fib(n) has F(n+1) leaves, where:

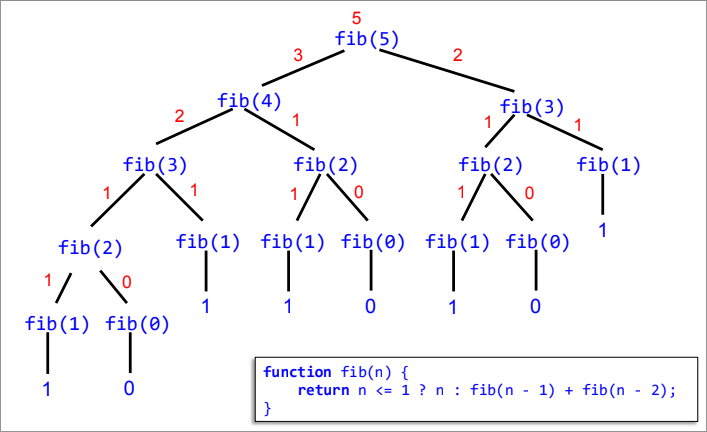
fib.png

  1. Iterative solution
js
function fib(n) {
	return fib_iter(1, 0, n);
}
function fib_iter(a, b, count) {
	// adding up the smaller values on the fib tree count times
	return count === 0
	? b
	: fib_iter(a + b, a, count - 1);
}

time, without “branching”